电磁场的数学表述

电磁场研究中使用了多种电磁场数学描述，电磁学是自然界的四种基本相互作用之一。 在这篇文章中，讨论了几种方法，尽管一般来说，这些方程是根据电场和磁场、电势和电流电荷来计算的。

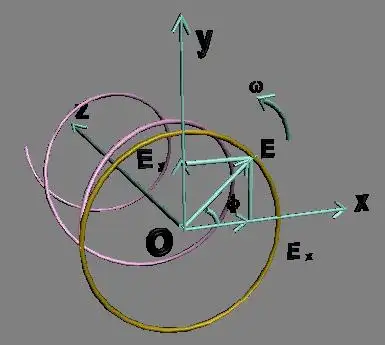
最常见的电磁场描述使用两个三维矢量场，称为电场和磁场。 这些矢量场每个都有一个在空间和时间的每个点定义的值，因此通常被视为空间和时间坐标的函数。 因此，它们通常写为 E(x, y, z, t)（电场）和 B(x, y, z, t)（磁场）。

如果只有电场 (E) 不为零且随时间恒定，则称该场为静电场。 类似地，如果只有磁场 (B) 不为零且随时间恒定，则称该场为静磁场。 但是，如果电场或磁场具有时间相关性，则必须使用麦克斯韦方程将这两个场一起视为耦合电磁场。

很多时候在电场和磁场的使用和计算中，使用的方法首先计算一个相关的势能：电场的电势 φ {displaystyle varphi } 和磁矢势 A，对于 磁场。 电势是标量场，而磁势是矢量场。 这就是为什么有时将电势称为标量势而将磁势称为矢量势的原因。

这些关系可以代入麦克斯韦方程组，用势能来表达后者。 法拉第定律和高斯磁定律（齐次方程）对任何势都同样成立。 这是因为场表示为标量势和矢量势的梯度和旋度的方式。 麦克斯韦方程的另外两个（非齐次方程）描述了潜在公式中的动力学。

这些方程放在一起就像麦克斯韦方程一样强大和完整。 此外，问题有所减少，因为电场和磁场总共有六个分量需要解决。