混合长理论

在流体动力学中，混合长度模型是一种试图通过涡粘性来描述牛顿流体边界层内湍流雷诺应力的动量传递的方法。 该模型由 Ludwig Prandtl 在 20 世纪初开发。 普朗特本人对该模型持保留态度，将其描述为只是一个粗略的近似值，但此后它已被用于许多领域，包括大气科学、海洋学和恒星结构。

混合长度在概念上类似于热力学中的平均自由程概念：在与周围流体混合之前，流体块将在特征长度 ξ ′ {displaystyle xi ‘} 内保持其属性。 Prandtl 描述了混合长度，

在每种情况下，可以将其视为整体移动的流体质量的直径； 或者，作为这种类型的质量在与邻近质量混合之前所经过的距离……

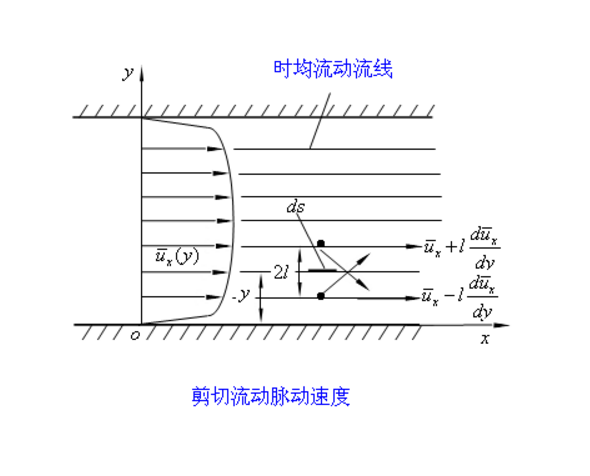
在上图中，当包裹在温度梯度上移动时，温度 T {displaystyle T} 在一定距离内是守恒的。 包裹在整个过程中经历的温度波动是 T ′ {displaystyle T’} 。 所以 T ′ {displaystyle T’} 可以看作是它移动超过这个混合长度 ξ ′ {displaystyle xi ‘} 后与周围环境的温度偏差。

首先，我们必须首先能够将数量表示为缓慢变化分量和波动分量的总和。

这个过程被称为雷诺分解。 温度可表示为：

T = T¯ + T ′ {displaystyle T={overline {T}}+T’} ,

其中 T ¯ {displaystyle {overline {T}}} 是缓慢变化的分量， T ′ {displaystyle T’} 是波动分量。

尽管这样做的理论依据较弱，因为压力梯度力会显着改变波动分量。 此外，对于垂直速度的情况， w ′ {displaystyle w’} 必须处于中性分层流体中。

取水平和垂直波动的乘积给我们：

u ′ w ′ ¯ = ξ ′ 2 ¯ | ∂ w ¯ ∂ z | ∂ u ¯ ∂ z {displaystyle {overline {u’w’}}={overline {xi ‘{2}}}left|{frac { partial {overline {w}}}{partial z}}right|{frac {partial {overline {u}}}{partial z}}} 。

涡流粘度由上式定义为：

K m = ξ ′ 2 ¯ | ∂ w ¯ ∂ z | {displaystyle K_{m}={overline {xi ‘{2}}}left|{frac {partial {overline {w}}}{ 部分 z}}right|} ，

所以我们有涡流粘度 K m {displaystyle K_{m}} 表示为混合长度， ξ ′ {displaystyle xi ‘} 。