最速降线问题

在物理学和数学中，最速曲线（源自古希腊语 βράχιστος χρόνος (brákhistos khrónos) ‘最短时间’）或最快下降曲线是位于点 A 和较低点 B 之间的平面上的曲线，其中 B不在A的正下方，珠子在均匀引力场的作用下无摩擦地滑动到给定的终点，时间最短。 这个问题是约翰·伯努利在 1696 年提出的。

最速同步曲线与等速同步曲线的形状相同； 两者都是摆线。 但是，用于两者的摆线部分各不相同。 更具体地说，brachistochrone 最多可以使用摆线的完整旋转（当 A 和 B 处于同一水平时的极限），但始终从尖点开始。 相比之下，tautochrone 问题最多只能使用前半个旋转，并且总是在水平方向结束。 该问题可以使用来自变分法和最优控制的工具来解决。

该曲线与测试体的质量和局部重力强度无关。 只选择一个参数，使曲线拟合起点 A 和终点 B。如果给定物体在 A 处的初始速度，或者如果考虑摩擦，则使时间最短的曲线不同于等时线曲线 .

约翰·伯努利 (Johann Bernoulli) 于 1696 年 6 月向 Acta Eruditorum 的读者提出了最速线的问题。他说：

我，约翰·伯努利，向世界上最杰出的数学家致辞。 对于聪明人来说，没有什么比一个诚实的、具有挑战性的问题更吸引人的了，其可能的解决方案将带来名声并成为永恒的纪念碑。 以帕斯卡、费马等人为榜样，我希望通过向我们这个时代最优秀的数学家提出一个考验他们的方法和智力的问题来赢得整个科学界的感激。 如果有人向我传达所提出问题的解决方案，我将公开宣布他值得表扬

伯努利将问题陈述写成：

给定垂直平面内的两点A、B，求一点仅受重力作用，从A点到B点所画出的曲线是什么？

Johann 和他的兄弟 Jakob Bernoulli 推导出了相同的解决方案，但是 Johann 的推导是错误的，他试图冒充 Jakob 的解决方案作为他自己的解决方案。 约翰于次年5月在期刊上发表了该解，并指出该解与惠更斯的等时线是同一条曲线。 在用下面给出的方法推导出曲线的微分方程后，他继续证明它确实产生了一个摆线。 然而，他的证明因使用单个常数而不是下面的三个常数 vm、2g 和 D 而受到损害。

伯努利允许六个月的时间来解决问题，但在此期间没有收到任何解决方案。 应莱布尼茨的要求，时间公开延长了一年半。 下午 4 点 1697 年 1 月 29 日，当艾萨克·牛顿从皇家铸币厂回到家中时，他在约翰·伯努利 (Johann Bernoulli) 的一封信中发现了挑战。 牛顿彻夜未眠求解，并在下一个帖子前匿名将解法邮寄了出去。 伯努利读完答案后，立刻认出了它的作者，并惊呼他从爪痕中认出了一只狮子。 这个故事让人们对牛顿的力量有了一些了解，因为约翰·伯努利花了两周的时间来解决它。 牛顿还写道，我不喜欢在数学的事情上被老外[纠缠]和取笑…，而且牛顿已经解决了牛顿的最小阻力问题，这被认为是变分法中的xxx个问题 .

最后，五位数学家给出了解决方案：牛顿、雅各布·伯努利、戈特弗里德·莱布尼茨、埃伦弗里德·瓦尔特·冯·契恩豪斯和纪尧姆·德·洛皮塔尔。 其中四个解决方案（不包括 l’Hôpital’s）与 Johann Bernoulli’s 发表在同一版本的期刊上。 在他的论文中，Jakob Bernoulli 在证明其解是摆线之前给出了与下面相似的最短时间条件证明。

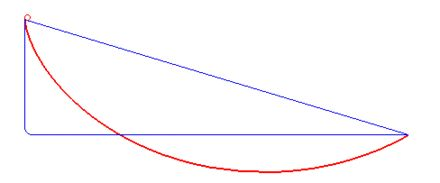
根据牛顿学者汤姆·怀特塞德的说法，为了超越他的兄弟，雅各布·伯努利创造了一个更难的最速长线问题版本。 在解决这个问题时，他开发了新的方法，这些方法被莱昂哈德·欧拉 (Leonhard Euler) 改进为后者所谓的（1766 年）变分法。 约瑟夫-路易斯·拉格朗日 (Joseph-Louis Lagrange) 做了进一步的工作，产生了现代微积分。

早些时候，在 1638 年，伽利略曾在他的两门新科学中试图解决一个类似的问题，即从一点到墙的最快下降路径。