兰贝格-奥斯古德关系
目录
兰贝格-奥斯古德关系
Ramberg-Osgood 方程的创建是为了描述材料在屈服点附近的应力和应变之间的非线性关系,即应力-应变曲线。 它特别适用于因塑性变形而硬化的金属(见加工硬化),表现出平滑的弹塑性转变。 由于它是一种现象学模型,因此必须针对感兴趣的特定材料检查模型与实际实验数据的拟合度。
ε {displaystyle varepsilon } 是应变,σ {displaystyle sigma } 是应力,E {displaystyle E} 是杨氏模量,K {displaystyle K} 和 n { displaystyle n} 是取决于所考虑材料的常量。 在这种形式下,K 和 n 与 Hollomon 方程中常见的常数不同。
该方程基本上假设应力-应变曲线的弹性应变部分 ε e {displaystyle varepsilon _{e}} 可以用一条线建模,而塑性部分 ε p {displaystyle varepsilon _{p}} ,可以用幂律建模。 将弹性分量和塑性分量相加得到总应变。
右边的xxx项 σ / E {displaystyle {sigma }/{E},} 等于应变的弹性部分,而第二项 K ( σ / E ) n {displaystyle K({sigma }/{E}){n}} ,占塑料部分,参数 K {displaystyle K} 和 n {displaystyle n} 描述硬化 材料的行为。
硬化行为和屈服偏移
在 Ramberg–Osgood 模型的最后一种形式中,材料的硬化行为取决于材料常数 α {displaystyle alpha ,} 和 n {displaystyle n,} 。 由于应力和塑性应变之间的幂律关系,Ramberg-Osgood 模型表明即使在非常低的应力水平下也存在塑性应变。 然而,对于低应力和材料常量 α {displaystyle alpha } 和 n {displaystyle n} 的常用值,与弹性应变相比,塑性应变仍然可以忽略不计。 另一方面,对于高于 σ 0 {displaystyle sigma _{0}} 的应力水平,塑性应变逐渐大于弹性应变。
n {displaystyle n,} 的常用值是 ~5 或更大,尽管通常通过拟合拉伸(或压缩)实验数据获得更精确的值。 α {displaystyle alpha ,} 的值也可以通过拟合实验数据找到,尽管对于某些材料,它可以被固定以使屈服偏移等于可接受的应变值 0.2%
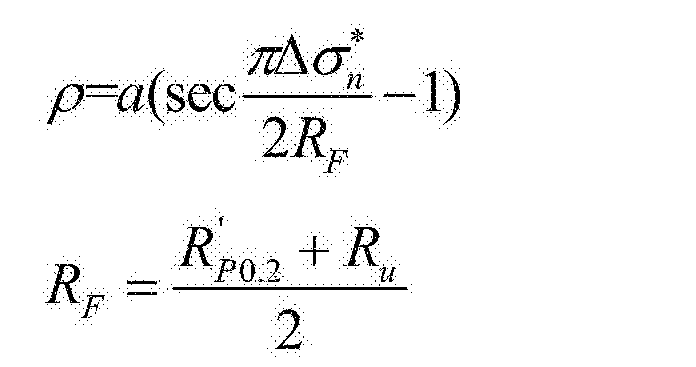
替代配方
可以找到 Ramberg-Osgood 方程的几种略有不同的替代公式。 由于模型纯粹是经验性的,因此尝试不同的模型并检查哪个模型最适合所选材料通常很有用。
Ramberg-Osgood 方程也可以使用 Hollomon 参数表示,其中 K {displaystyle K} 是强度系数 (Pa),n {displaystyle n} 是应变硬化系数(无单位)。