鞍结点分岔

在分岔理论的数学领域中，鞍结分岔、切向分岔或褶皱分岔是动力系统的两个固定点（或平衡点）相互碰撞和湮灭的局部分岔。 术语“鞍点分岔”最常用于指代连续动力系统。 在离散动力系统中，相同的分岔通常被称为折叠分岔。 另一个名字是蓝天分叉，指的是两个固定点的突然产生。

如果相空间是一维的，平衡点之一不稳定（鞍点），而另一个平衡点稳定（节点）。

熔结点分岐可能与滞后回路和灾难有关。

具有鞍结点分岔的微分方程的典型示例是：

d x d t = r + x 2 。 {displaystyle {frac {dx}{dt}}=r+x{2}。}

这里 x {displaystyle x} 是状态变量， r {displaystyle r} 是分岔参数。

• 如果 r < 0 {displaystyle r<0} 有两个平衡点，一个稳定的平衡点在 − − r {displaystyle -{sqrt {-r}}} 和一个不稳定的平衡点在 + − r {displaystyle +{sqrt {-r}}} .
• 在 r = 0 {displaystyle r=0}（分叉点）处，只有一个平衡点。 此时不动点不再是双曲线。 在这种情况下，固定点称为鞍节点固定点。
• 如果 r > 0 {displaystyle r>0} 没有平衡点。

在二维动力系统中出现二维鞍节点分叉

从通过改变参数 α {displaystyle alpha } 绘制相图获得的动画可以看出，

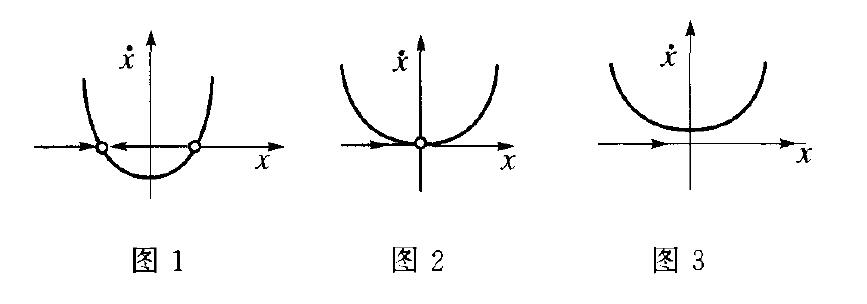
如果消耗项从 p x {displaystyle px} 变为 p {displaystyle p} ，即消耗率恒定而不 与资源 x {displaystyle x} 的比例。

其他示例是对生物开关进行建模。 最近表明，在某些条件下，广义相对论的爱因斯坦场方程与折叠分岔具有相同的形式。 还研究了鞍节点分叉的非自主版本（即参数是时间相关的）。