恒定振幅零自相关波形

在信号处理中，恒定振幅零自相关波形（CAZAC）是一个周期性的复值信号，模数为1，相位外的周期性（循环）自相关等于零。CAZAC序列在无线通信系统中找到了应用，例如在3GPP长期演进中用于移动电话与基站的同步。Zadoff-Chu序列是著名的CAZAC序列，具有特殊的属性。CAZAC序列的功率谱CAZAC序列的功率谱是平的。

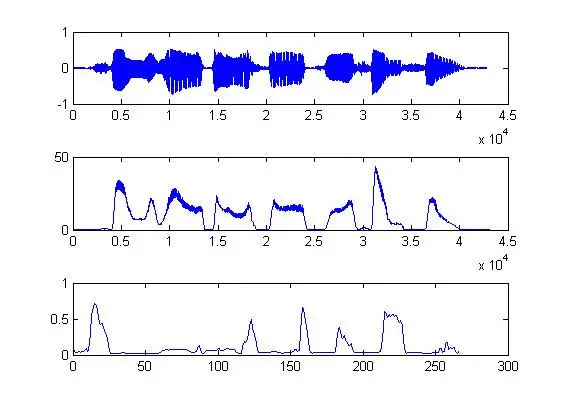
如果我们有一个CAZAC序列，时域自相关是一个脉冲r(τ)=δ(n){displaystyler(tau)=delta(n)}。自相关的离散傅里叶变换是平的R(f)=1/N{displaystyleR(f)=1/N}。