大边际近邻
目录
简介
大边际近邻(LMNN)分类是一种用于度量学习的统计机器学习算法。它学习的是一种为k-近邻分类设计的伪计量。该算法基于半有限编程,是凸式优化的一个子类。
监督学习(更具体地说是分类)的目标是学习一个决策规则,可以将数据实例归入预先定义的类别。k-近邻规则假定有一个标记实例的训练数据集(即已知的类别)。
它将一个新的数据实例归入由最接近(标记)的K个训练实例的多数投票所得到的类别。紧密性是用一个预先定义的指标来衡量的。大边际近邻是一种算法,它以监督的方式学习这个全局(伪)度量,以提高k-近邻规则的分类精度。
大边际近邻的设置
LMNN背后的主要直觉是学习一个伪度量,在这个伪度量下,训练集中的所有数据实例都被至少k个共享相同类别标签的实例包围。如果能做到这一点,就能使撇开误差(交叉验证的一种特殊情况)最小化。让训练数据由一个数据集组成{displaystyled(cdot,cdot)}的定义是正确的,矩阵M{displaystylemathbf{M}}。}需要是正半定的。欧几里德公制是一个特例,其中{displaystyle`mathbf{M}}是一个特殊的例子。}是身份矩阵。这种泛化通常(错误地)被称为Mahalanobis度量。图1说明了该公制在变化的情况下的效果{displaystylemathbf{M}}的影响。}.两个圆圈显示的是与中心距离相等的点的集合.在欧几里得情况下,这个集合是一个圆,而在修正的(Mahalanobis)度量下,它变成了一个椭圆体。该算法区分了两类特殊数据点:目标邻居和冒名顶替者。
目标邻居
目标邻居在学习之前就被选中。每个实例.目标邻居是指在学到的度量下应该成为最近邻居的数据点。让我们来表示一个数据点的目标邻居的集合.在学习过程中,该算法试图使训练集中所有数据实例的冒名顶替者的数量最小。算法大边际近邻优化了矩阵借助于半无限编程。其目标是双重的。对于每个数据点{displaystyle{vec{x}}_{i}},目标邻居应该接近,而冒名顶替者应该远离。
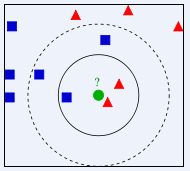
目标邻居应该是接近的,而冒牌货应该是远离的。图1显示了这种优化对一个说明性例子的影响。学习到的度量使输入向量{displaystyle{vec{x}}_{i}}的输入向量被包围。被同一类别的训练实例所包围。