歧义语法

在计算机科学中，歧义语法是指存在一个可以有多个最左派生或解析树的字符串的无背景语法，而非歧义语法是指每个有效字符串都有xxx的最左派生或解析树的无背景语法。许多语言同时承认模糊和不模糊的语法，而有些语言只承认模糊的语法。任何非空语言都可以通过采用一个不含糊的语法并引入一个重复的规则或同义词来接纳一个含糊的语法（xxx没有含糊语法的语言是空语言）。一种只接受模棱两可的语法的语言被称为固有模棱两可的语言，而且有固有模棱两可的无语境语言。确定性的无语境语法总是无歧义的，是无歧义语法的一个重要子类；但也有非确定的无歧义语法。对于计算机编程语言来说，由于诸如danglingelse的问题，参考语法往往是模糊的。如果存在这些含糊不清的地方，一般通过增加优先级规则或其他上下文敏感的解析规则来解决，所以整个短语语法是不含糊的。一些解析算法（如（Earley或GLR解析器）可以从语法上有歧义的字符串中生成解析树（或解析森林）的集合。

微不足道的语言最简单的例子是下面这个微不足道的语言的模糊语法（起始符号为A），它只由空字符串组成。A→A|ε……意思是说，非终端A可以再次派生到它本身，或者派生到空字符串。因此，空字符串的最左派生长度为1、2、3，甚至是任何长度，这取决于A→A规则被使用了多少次。这种语言也有一个毫不含糊的语法，由一条生产规则组成。A→ε……这意味着xxx的生产只能产生空字符串，也就是语言中xxx的字符串。同样，任何非空语言的语法都可以通过增加重复的内容而变得含糊不清。单一字符串一个给定字符的单数字符串的正则语言，例如’a’（正则表达式a*），具有无歧义的语法。A→aA|ε…但也有模棱两可的语法。A→aA|Aa|ε这些对应于产生一个右关联树（对于非明确的语法）或允许左关联和右关联。这一点将在下文详述。加法和减法语境自由语法A→A+A|A-A|a是模糊的，因为字符串a+a+a有两个最左边的派生。再比如，该语法是不明确的，因为字符串a+a-a有两个解析树。然而，它所生成的语言本质上并不含糊；下面是一个生成相同语言的非含糊语法。

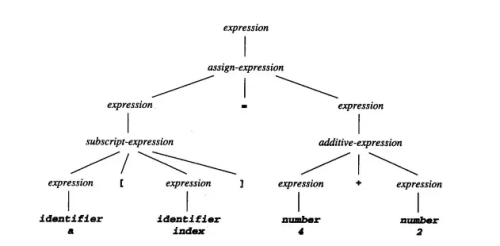
A→A+a|A-a|a悬空的else计算机编程语言中一个常见的模糊性例子是悬空的else问题。在许多语言中，If-then(-else)语句中的else是可选的，这导致嵌套条件在无语境语法方面有多种识别方式。具体来说，在许多语言中，人们可以用两种有效的形式来写条件句：If-then形式和If-then-else形式–实际上，使else子句是可选的。这在不同的语言中以不同的方式解决。有时语法被修改，使其不含糊，例如要求有endif语句或使else成为强制性的。在其他情况下，语法是模棱两可的，但模棱两可的解决方法是使整个短语的语法对上下文敏感，例如将else与最近的if联系起来。在后一种情况下，语法是不含糊的，但无语境语法是含糊的。

同一字符串的多个派生的存在并不足以表明语法是歧义的；只有最左边的多个派生（或者，等同于多个解析树）才表明歧义。是语言{0+0,0+1,1+0,1+1}的一个无歧义的语法。虽然这四个字符串中的每一个只有一个最左边的派生，但它有两个不同的派生，例如s⇒a+a⇒0+a⇒0+0和s⇒a+a⇒a+0⇒0+0只有前一个派生是最左边的。