DFT矩阵
词条百科 0
目录
DFT矩阵
在应用数学中,DFT矩阵是离散傅里叶变换(DFT)作为一个变换矩阵的表达,它可以通过矩阵乘法应用于信号。
DFT矩阵的定义
一个N点的DFT表示为乘法{displaystyleomega{x}=omega{xmodN}。这是统一根的Vandermonde矩阵,直到归一化因子。请注意,和前面的归一化因子({displaystyle1/{sqrt{N}}}和前面的归一化系数(1/N))和ω中指数的符号只是惯例,在某些处理中有所不同。下面所有的讨论都适用于任何惯例,最多只需稍作调整。xxx重要的是,正变换和反变换的指数是相反的,而且它们的归一化因子的乘积是1/N。然而,这{displaystyle1/{sqrt{N}}的选择使产生的DFT矩阵成为一个单元。}这里的选择使得所产生的DFT矩阵是单一的,这在许多情况下是很方便的。快速傅里叶变换算法利用矩阵的对称性来减少向量与该矩阵相乘的时间,从通常的.类似的技术也可以应用于矩阵的乘法,如Hadamard矩阵和Walsh矩阵。
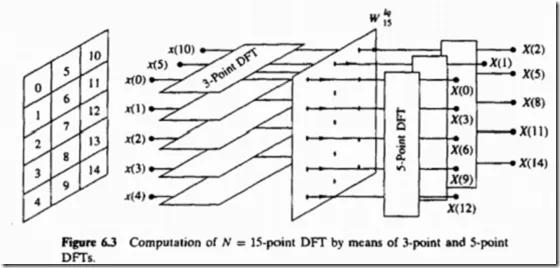
DFT矩阵的例子
两点
两点DFT是一个简单的例子,其中xxx个条目是DC(和),第二个条目是AC(差)。xxx行执行的是和,第二行执行的是差。{displaystyle1/{sqrt{2}}的系数是为了使变换成为统一的。}是为了使变换成为单一的。
内容来源于网络,本内容不代表16map.com立场,内容投诉举报请联系16map.com客服。如若转载,请注明出处:https://16map.com/wiki/nmteyi3lnidi