斯特里贝克曲线
目录
简介
斯特里贝克曲线是摩擦学领域的一个基本概念。 它表明流体润滑接触中的摩擦是接触载荷、润滑剂粘度和润滑剂夹带速度的非线性函数。 这一发现和基础研究通常归功于 Richard Stribeck 和 Mayo D. Hersey,他们在 20 世纪上半叶研究了铁路货车轴颈轴承的摩擦; 然而,其他研究人员之前也得出了类似的结论。
概念
对于两个流体润滑表面的接触,斯特里贝克曲线显示了所谓的赫赛数(无量纲润滑参数)与摩擦系数之间的关系。 赫西数定义为:
赫西数 = η ⋅ N P , {displaystyle {begin{aligned}{text{赫西数}}={frac {eta cdot N}{P}},end{ 对齐}}}
其中 η 是流体的动态粘度,N 是流体的夹带速度,P 是每单位摩擦接触长度的法向载荷。
Hersey 的原始公式使用 N 的转速(每单位时间的转数)和 P 的单位投影面积的负载(即轴颈轴承的长度和直径的乘积)。
或者,Hersey 数是从速度 (m/s) 乘以动态粘度 (Pa∙s = N∙s/m2) 除以每单位轴承长度的载荷 (N/m) 得到的无量纲数。
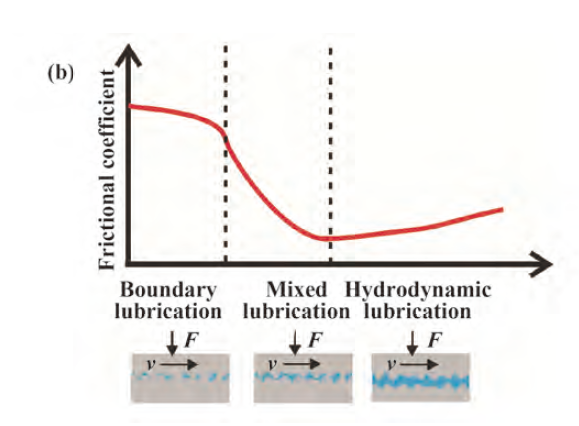
因此,对于给定的粘度和负载,斯特里贝克曲线显示了摩擦如何随着速度的增加而变化。 根据斯特里贝克曲线(见右图)的典型进展,可以确定三种润滑方式。
历史
Richard Stribeck 的研究在柏林的皇家普鲁士技术测试研究所(MPA,现为 BAM)进行,他的研究结果于 1901 年 12 月 5 日在铁路协会的公开会议上公布,并于 1902 年 9 月 6 日发表。类似的工作 先前由 Adolf Martens 在同一研究所于 1885 年左右进行,并且在 1870 年代中期由美国史蒂文斯理工学院的 Robert Henry Thurston 进行。液体润滑表面的摩擦曲线形式的原因后来归因于 Stribeck——尽管 Thurston 和 Martens 都相当早地取得了他们的成果——可能是因为 Stribeck 在当时德国最重要的技术期刊 Zeitschrift des Vereins Deutscher Ingenieure(VDI,德国机械工程师杂志)上发表了他的发现。 Martens 在皇家普鲁士技术测试研究所(现已更名为 BAM)的官方期刊上发表了他的研究结果。 VDI 期刊提供了对 Stribeck 数据的广泛访问,后来的同事将结果合理化为三种经典摩擦机制。 瑟斯顿没有实验方法来记录摩擦系数的连续图,只能在离散点上进行测量。 这可能就是为什么他没有发现液体润滑轴颈轴承的最小摩擦系数,而是通过 Martens 和 Stribeck 的图表证明的原因。
Martens 绘制的图表显示了摩擦系数作为压力、速度或温度(即粘度)的函数,但不是它们与赫塞数的组合。 Schmidt 试图使用 Marten 的数据来做到这一点。 曲线的特征最小值似乎对应于 0.00005-0.00015 范围内的非常低的 Hersey 数。
Stribeck曲线的计算
一般来说,在所有润滑状态下,斯特里贝克曲线的计算有两种方法。 在xxx种方法中,控制流动和表面变形方程(弹性流体动力润滑方程组)通过数值求解。 尽管数值解可能相对准确,但这种方法计算量大且需要大量计算资源。 第二种方法依赖于负载共享概念,该概念可用于近似解决问题,但计算成本要低得多。