埃瓦尔德求和
目录
简介
埃瓦尔德求和,以 Paul Peter Ewald 的名字命名,是一种计算周期性系统中长程相互作用(例如静电相互作用)的方法。它最初是作为计算离子晶体静电能的方法开发的,现在通常用于计算计算化学中的长程相互作用。埃瓦尔德求和是泊松求和公式的一个特例,用傅立叶空间中的等效求和代替实空间中相互作用能的求和。在该方法中,长程相互作用分为两部分:短程贡献和不具有奇点的长程贡献。短程贡献是在实空间中计算的,而长程贡献是使用傅里叶变换计算的。与直接求和相比,这种方法的优点是能量收敛迅速。这意味着该方法在计算长程相互作用时具有较高的精度和合理的速度,因此它是计算周期系统长程相互作用的事实上的标准方法。该方法需要分子系统的电荷中性,以便准确计算总库仑相互作用。Kolafa 和 Perram 对无序点电荷系统的能量和力计算中引入的截断误差进行了研究。
推导
埃瓦尔德求和将相互作用势重写为两项之和,
φ ( r ) = d e f φ s r ( r ) + φ ℓ r ( r ) {displaystyle varphi (mathbf {r} ) {stackrel {mathrm {def} }{=} } varphi _{sr}(mathbf {r} )+varphi _{ell r}(mathbf {r} )},
其中 φ s r ( r ) {displaystyle varphi _{sr}(mathbf {r} )} 表示其和在实空间中快速收敛的短程项,而 φ ℓ r ( r ) {displaystyle varphi _{ell r}(mathbf {r} )} 表示其和在傅立叶(倒数)空间中快速收敛的长程项。 对于所有参数(最明显的是 r = 0),长程部分应该是有限的,但可以有任何方便的数学形式,最典型的是高斯分布。该方法假设短程部分可以很容易地求和; 因此,问题变成了长期项的总和。 由于使用傅里叶和,该方法隐含地假设所研究的系统是无限周期的(对晶体内部的合理假设)。这个假设的周期系统的一个重复单元称为晶胞。选择一个这样的单元格作为参考的中心单元格,其余单元格称为图像。
长程相互作用能是中心晶胞电荷与晶格所有电荷之间相互作用能的总和。 因此,它可以表示为代表晶胞场和晶格场的两个电荷密度场的二重积分
E ℓ r = ∬ d r d r ′ ρ TOT ( r ) ρ u c ( r ′ ) φ ℓ r ( r − r ′ ) {displaystyle E_{ell r}=iint dmathbf {r} ,dmathbf {r} {prime },rho _{text{TOT}}(mathbf {r} )rho _{uc}(mathbf {r } {prime }) varphi _{ell r}(mathbf {r} -mathbf {r} {prime })}
其中晶胞电荷密度场 ρ u c ( r ) {displaystyle rho _{uc}(mathbf {r} )} 是位置 r k {displaystyle mathbf {r} _{k}} 电荷 q k {displaystyle q_{k}} 在中央晶胞中
ρ u c ( r ) = d e f ∑ c h a r g e s k q k δ ( r − r k ) {displaystyle rho _{uc}(mathbf {r} ) {stackrel {mathrm {def} }{ =}} sum _{mathrm {charges} k}q_{k}delta (mathbf {r} -mathbf {r} _{k})}
并且总电荷密度场 ρ TOT ( r ) {displaystyle rho _{text{TOT}}(mathbf {r} )} 与晶胞电荷 q k { displaystyle q_{k}} 及其周期图像
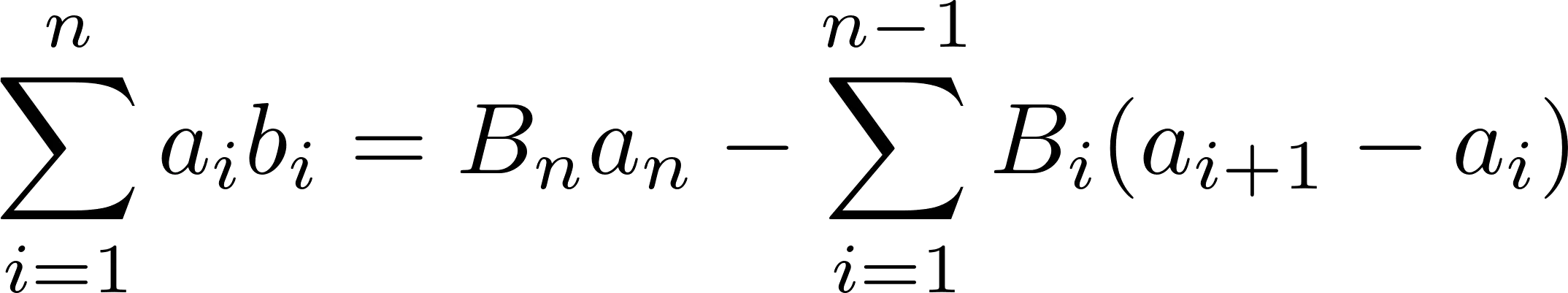
ρ TOT ( r ) = d e f ∑ n 1 , n 2 , n 3 ∑ c h a r g e s k q k δ ( r − r k − n 1 a 1 − n 2 a 2 − n 3 a 3 ) {displaystyle rho _{ text{TOT}}(mathbf {r} ) {stackrel {mathrm {def} }{=}} sum _{n_{1},n_{2},n_ {3}}sum _{mathrm {charges} k}q_{k}delta (mathbf {r} -mathbf {r} _{k}-n_{1} mathbf {a} _{1}-n_{2}mathbf {a} _{2}-n_{3}mathbf {a} _{3})}
这里, δ ( x ) {displaystyle delta (mathbf {x} )} 是狄拉克delta函数, a 1 {displaystyle mathbf {a} _{1}} , a 2 { displaystyle mathbf {a} _{2}} 和 a 3 {displaystyle mathbf {a} _{3}} 是点阵向量,n 1 {displaystyle n_{1}} , n 2 {displaystyle n_{2}} 和 n 3 {displaystyle n_{3}} 在所有整数范围内。总场 ρ TOT ( r ) {displaystyle rho _{text{TOT}}(mathbf {r} )} 可以表示为 ρ u c ( r ) {displaystyle rho _{uc}(mathbf {r} )} 具有格函数 L ( r ) {displaystyle L(mathbf {r} )}。