声学度规

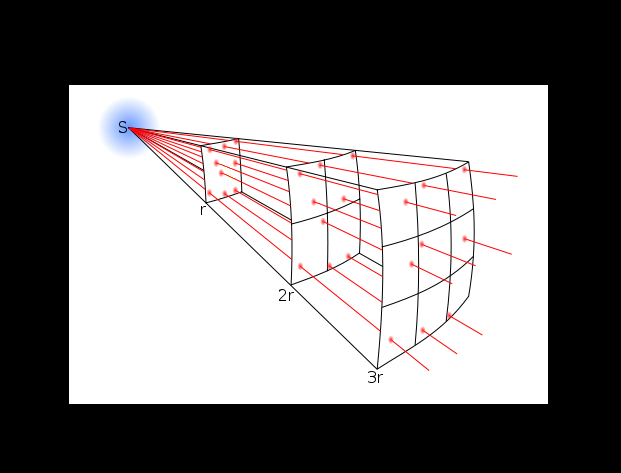
在数学物理学中，度量描述了表面或体积内相对距离的排列，通常由穿过该区域的信号测量——本质上描述了该区域的固有几何形状。 声学度量将描述给定颗粒介质在声学或流体动力学中的信号传输特性。 有时也可以互换使用其他描述性名称，例如声波度量。

为简单起见，我们假设底层背景几何是欧几里德几何，并且该空间充满零温度下各向同性的无粘流体（例如超流体）。 这种流体由密度场 ρ 和速度场 v → {displaystyle {vec {v}}} 描述。 任何给定点的声速取决于可压缩性，而可压缩性又取决于该点的密度。 将更多的东西压缩到已经紧凑的空间中需要做很多工作。 这可以通过声场c的速度来指定。

如果我们想象声音就像光在一个称为声学度量的有效度量张量描述的时空中移动，那么这种限制也会出现。

声学度量可以产生声学视界（也称为声波视界），类似于广义相对论时空度量中的事件视界。 然而，与时空度量不同，其中不变速度是所有因果效应传播的xxx上限，声学度量中的不变速度不是传播速度的上限。 例如，声速小于光速。 因此，声学度量中的视界与时空度量中的视界并不完全相似。 某些物理效应可能会跨过声学视界反向传播。 这种传播有时被认为类似于霍金辐射，尽管后者是由弯曲时空中的量子场效应引起的。

由于声学度量与我们预期未来量子引力理论的行为方式（例如霍金辐射）有一些统计行为，因此有时会研究这些度量，希望它们可以揭示实际黑洞的统计力学 . 有人认为模拟模型不仅仅是一个类比，我们观察到的实际引力实际上是一个模拟理论。 但为了保持这一点，由于通用模拟模型取决于声学度量和底层背景几何，理论的低能量大波长限制必须与背景几何分离。