角速度

在物理学中，角速度或旋转速度（ω 或 Ω），也称为角频率矢量，是一个伪矢量表示对象的角位置或方向随时间变化的速度（即对象旋转或公转相对于 点或轴）。 伪矢量的大小表示角速度，即物体旋转或公转的速率，其方向垂直于瞬时旋转平面或角位移。 角速度的方向通常由右手法则指定。

有两种类型的角速度。

• 轨道角速度是指一个点物体绕固定原点旋转的速度，即它的角位置相对于原点的时间变化率。
• 自旋角速度是指刚体相对于其旋转中心旋转的速度，与轨道角速度相反，与原点的选择无关。

通常，角速度具有每单位时间角度的量纲（角度用时间代替线速度的距离）。 角速度的SI单位是弧度每秒，弧度是无量纲量，因此角速度的SI单位可以列为s-1。 角速度通常用符号 omega（ω，有时是 Ω）表示。 按照惯例，正角速度表示逆时针旋转，而负角速度表示顺时针旋转。

例如，地球静止卫星每天在赤道上方完成一个轨道，或每 24 小时 360 度，并且角速度 ω = (360°)/(24 h) = 15°/h，或 (2π rad)/( 24 小时）≈ 0.26 弧度/小时。 如果角度以弧度为单位，则线速度是半径乘以角速度，v = r ω {displaystyle v=romega } 。 轨道半径距地球中心 42,000 公里，因此卫星在太空中的速度为 v = 42,000 公里 × 0.26/h ≈ 11,000 公里/小时。 由于卫星随着地球自转向东运行（从北极上方逆时针方向），因此角速度为正。

在半径为 r {displaystyle r} 的圆周运动的最简单情况下，位置由距 x 轴的角位移 ϕ ( t ) {displaystyle phi (t)} 给出，轨道角速度为 角度相对于时间的变化率：ω = d ϕ d t {textstyle omega ={frac {dphi }{dt}}} 。 如果 ϕ {displaystyle phi } 以弧度测量，则从围绕圆的正 x 轴到粒子的弧长为 ℓ = r ϕ {displaystyle ell =rphi } ， 线速度为 v ( t ) = d ℓ d t = r ω ( t ) {textstyle v(t)={frac {dell }{dt}}=romega (t) } ，因此 ω = v r {textstyle omega ={frac {v}{r}}} 。

在粒子在平面内运动的一般情况下，轨道角速度是相对于选定原点的位置矢量扫出角度的速率。 该图显示了从原点 O {displaystyle O} 到粒子 P {displaystyle P} 的位置向量 r {displaystyle mathbf {r} } ，其极坐标（ r ， ϕ ）{ displaystyle (r,phi )} 。 （所有变量都是时间 t {displaystyle t} 的函数。）粒子的线速度分裂为 v = v ‖ + v ⊥ {displaystyle mathbf {v} =mathbf {v} _{ |}+mathbf {v} _{perp }} ，径向分量 v ‖ {displaystyle mathbf {v} _{|}} 平行于半径，交叉 径向（或切向）分量 v ⊥ {displaystyle mathbf {v} _{perp }} 垂直于半径。 当没有径向分量时，粒子绕原点作圆周运动； 但当没有交叉径向分量时，它从原点沿直线移动。 由于径向运动使角度不变，因此只有线速度的交叉径向分量对角速度有贡献。

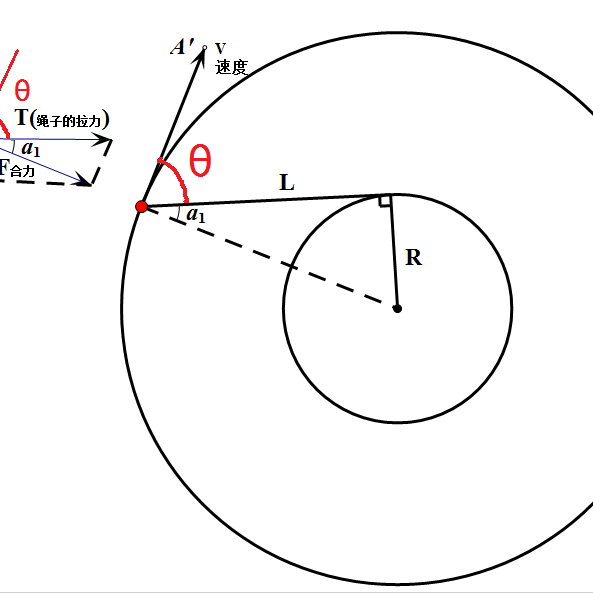
角速度 ω 是角位置相对于时间的变化率

这里的交叉径向速度 v ⊥ {displaystyle v_{perp }} 是 v ⊥ {displaystyle mathbf {v} _{perp }} 的有符号大小，逆时针运动为正 , 顺时针为负。 取线速度 v {displaystyle mathbf {v} } 的极坐标给出相对于半径向量的大小 v {displaystyle v} （线速度）和角度 θ {displaystyle theta }

这些公式可以推导出来做 varphi ))} ，是 r {displaystyle r} 到原点 wi 的距离的函数。