概率数值学

概率数值学是统计学、机器学习和应用数学交叉的一个科学领域，其中数值分析的任务包括寻找积分、线性代数、优化和微分方程的数值解，被视为统计、概率或贝叶斯推断的问题。

数值方法是一种近似于数学问题解决方案的算法（下面的例子包括线性方程组的解、积分的值、微分方程的解、多变量函数的最小值）。在概率数值算法中，这个逼近的过程被认为是一个估计、推理或学习的问题，并在概率推理的框架内实现（通常，但不总是贝叶斯推理）。从形式上看，这意味着用先验分布来设置计算问题，用似然函数来表述计算机计算的数字（例如线性代数中的矩阵-向量乘法、优化中的梯度、积分或定义微分方程的向量场的值）与有关数量（线性问题的解、最小值、积分、解曲线）之间的关系，并将后验分布作为输出。在大多数情况下，数值算法也会对要计算的数字进行内部自适应决策，这就形成了一个主动学习问题。许多最流行的经典数值算法可以在概率框架内重新解释。这包括共轭梯度法、Nordsieck方法、高斯正交规则和准牛顿方法。在所有这些情况下，经典的方法都是基于正则化的最小二乘估计，可以与高斯先验和似然产生的后验平均数相关联。在这种情况下，高斯后验的方差就与平方误差的最坏情况估计有关。与经典的基于点估计的近似技术相比，概率数字方法有几个概念上的优势。

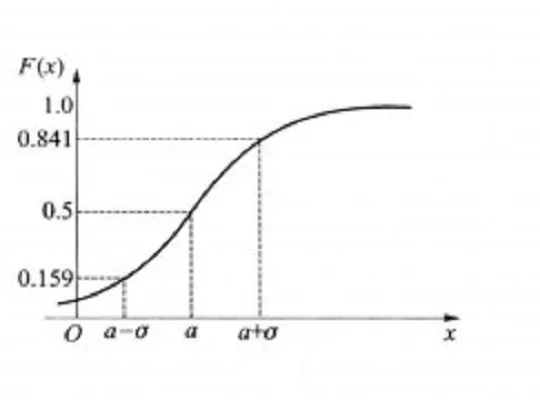
它们返回结构化的误差估计（特别是返回联合后验样本的能力，即对问题的真实未知解的多个现实假设）分级贝叶斯推理可以用来在这种方法中以通用的方式设置和控制内部超参数，而不是为每个参数重新发明新的方法由于它们使用并允许明确的似然描述计算的数字和目标数量之间的关系，概率数值方法甚至可以使用高度不精确、有偏见和随机的计算结果。相反，概率数值方法也可以在通常被认为没有可能性的计算中提供可能性，因为所有的概率数值方法基本上使用相同的数据类型–概率度量–来量化输入和输出的不确定性，它们可以被串联起来，在大规模的综合计算中传播不确定性。这些优势基本上等同于贝叶斯方法相对于机器学习中的点估计所享有的类似功能优势，应用或转移到计算领域。

已经为数值积分问题开发了概率数值方法，其中最流行的方法称为贝叶斯正交法。在数值积分中，函数的评价最常见的先验选择是高斯过程，因为这允许我们得到一个封闭式的积分后验分布，这是一个单变量的高斯分布。贝叶斯正交在以下情况下特别有用