切比雪夫伪谱法
词条百科 6
目录
切比雪夫伪谱法
用于最优控制问题的切比雪夫伪谱法是基于xxx类切比雪夫多项式。它是更大的伪谱最优控制理论的一部分,这个术语是由Ross创造的。与Legendre伪谱方法不同,Chebyshev伪谱(PS)方法并不能立即提供高精度的正交解。因此,该方法有两个不同的版本:一个由Elnagar等人提出,另一个由Fahroo和Ross提出。这两个版本在正交技术上有所不同。由于Clenshaw-Curtis正交技术易于实施(与Elnagar-Kazemi的单元平均法相比),Fahroo-Ross方法目前更常被使用。
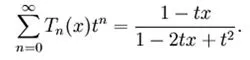
2008年,Trefethen表明Clenshaw-Curtis方法几乎与高斯正交一样精确。这一突破性的结果为切比雪夫PS方法的凹槽映射定理打开了大门。2009年,Gong、Ross和Fahroo终于为切比雪夫PS方法建立了一个完整的数学理论。
其他切比雪夫方法
切比雪夫PS方法经常与其他切比雪夫方法相混淆。在PS方法出现之前,许多作者提出使用切比雪夫多项式来解决最优控制问题;然而,这些方法都不属于伪谱方法的范畴。
内容来源于网络,本内容不代表16map.com立场,内容投诉举报请联系16map.com客服。如若转载,请注明出处:https://16map.com/wiki/nmteyi5loite