有序加权平均聚合算子

在应用数学中–特别是在模糊逻辑中–有序加权平均（OWA）算子提供了一个参数化的平均型聚合算子类别。它们是由RonaldR.Yager引入的。

许多著名的平均数运算符，如最 大、算术平均、中位数和最 小，都是这一类的成员。它们在计算智能中被广泛使用，因为它们有能力对语言表达的聚合指令进行建模。

正式的OWA算子的维度是通过选择不同的W，可以实现不同的聚合算子。由于确定bj的过程，OWA算子是一个非线性算子。属性OWA算子是一个平均算子。它是有界的、单调的、对称的和同位的，定义如下。著名的OWA算子此外，A-C(max)=1，A-C(ave)=A-C(med)=0.5，A-C(min)=0，因此，当我们从Max到Min聚合时，A-C从1到0。态度上的特点是聚合与OR操作的相似性（OR被定义为最 大）。第二个特征是分散性。

这定义为第 一类OWA聚合运算符上述Yager的OWA运算符被用来聚合清脆的数值。我们能在OWA机制中聚合模糊集吗？为此，第 一类OWA运算符被提出。

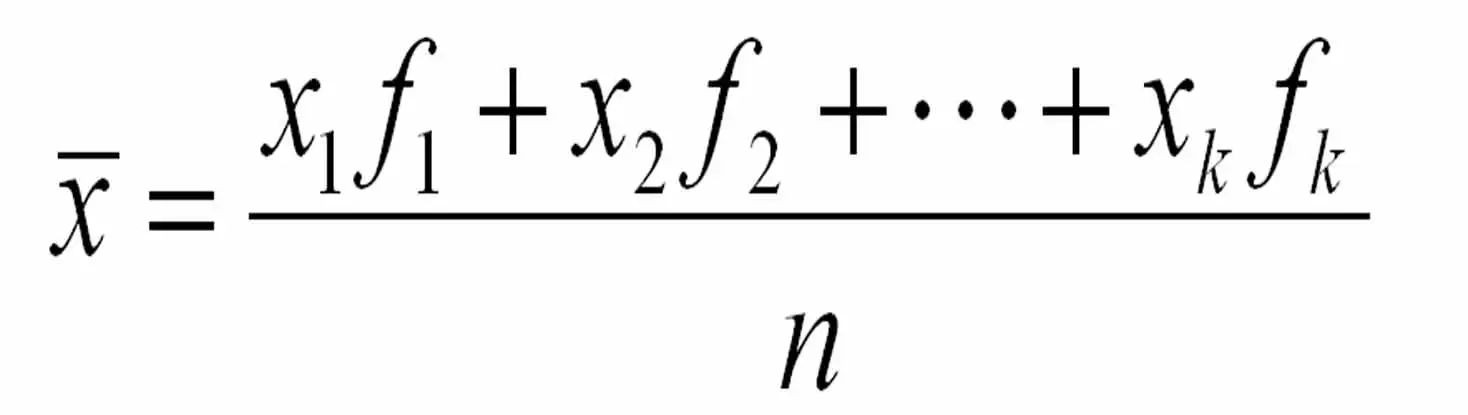
因此，第 一类OWA算子为我们提供了一种新的技术，在软决策和数据挖掘中，通过OWA机制直接聚合具有不确定权重的不确定信息，这些不确定对象由模糊集建模。第 一类OWA算子是根据模糊集的α-切面定义的，具体如下。给定n个语言权重{displaystyleU=[0,;;1]}，那么，对于每个人来说，都有一个定义在话语领域的模糊集。