奈奎斯特ISI准则
目录
奈奎斯特ISI准则
在通信领域,奈奎斯特ISI准则描述了当通信信道(包括发射和接收滤波器的响应)满足时,导致无符号间干扰或ISI的条件。它提供了一种构建带限函数的方法来克服符号间干扰的影响。当连续的符号通过线性调制(如ASK、QAM等)在信道上传输时,信道的脉冲响应(或等同于频率响应)会导致传输符号在时域上的扩散。这就造成了符号间干扰,因为之前传输的符号会影响当前接收的符号,从而降低了对噪声的容忍度。奈奎斯特定理将这个时域条件与一个等效的频域条件联系起来。奈奎斯特准则与奈奎斯特-香农采样定理密切相关,只是观点不同。
奈奎斯特准则
如果我们把信道的脉冲响应表示为这个标准可以用以下方式直观地理解:频率偏移的复制的H(f){displaystyleH(f)}的频率偏移复制品必须加到一个常数。必须加起来是一个常数。这个条件在以下情况下得到满足H(f){displaystyleH(f)}的频谱具有偶数对称性,其带宽小于或等于。频谱具有偶数对称性,其带宽小于或等于在实践中,这一准则被应用于基带滤波,将符号序列视为加权脉冲(狄拉克三角函数)。当通信系统中的基带滤波器满足奈奎斯特准则时,符号可以在有限的频段内以平坦的响应在信道上传输,而不会出现ISI。这种基带滤波器的例子是升余正弦滤波器,或理想情况下的sinc滤波器。
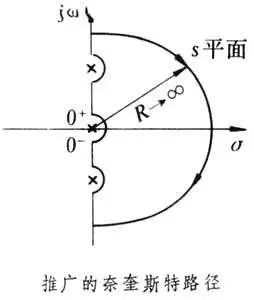
奈奎斯特ISI准则的推导
为了推导出该准则,我们首先用发射符号和信道响应来表示接收信号。让函数h(t)为信道脉冲响应,x[n]为要发送的符号,符号周期为Ts;接收信号y(t)的形式为(为简单起见,忽略了噪声)。在采样时刻,只有一个传输符号对接收的y[k]有影响,从而消除了任何ISI。这就是无ISI信道的时域条件。现在我们为它找到一个频域的等价物。我们首先用连续时间来表达这个条件。这相当于如上所述对响应进行采样,但使用的是连续时间表达式。然后条件的右边可以表示为原点的一个脉冲。{displaystyle{frac{1}{T_{s}}}{sum_{k=-infty}{+infty}Hleft(