H-infinity控制

H∞（即 H-infinity）方法在控制理论中用于合成控制器，以实现稳定并保证性能。 要使用 H∞ 方法，控制设计人员将控制问题表示为数学优化问题，然后找到解决此优化问题的控制器。 H∞ 技术优于经典控制技术，因为 H∞ 技术很容易适用于涉及通道间交叉耦合的多变量系统的问题； H∞ 技术的缺点包括成功应用它们所需的数学理解水平以及对要控制的系统的相当好的模型的需要。 重要的是要记住，由此产生的控制器仅在规定的成本函数方面是最优的，并不一定代表用于评估控制器的常用性能指标（例如稳定时间、能量消耗等）方面的最佳控制器。 此外，诸如饱和度之类的非线性约束通常无法很好地处理。

短语 H∞ 控制来自进行优化的数学空间的名称：H∞ 是矩阵值函数的哈代空间，这些函数是解析的并且有界于由 Re( s）> 0; H∞ 范数是函数在该空间上的xxx奇异值。 （这可以解释为任何方向和任何频率的xxx增益；对于 SISO 系统，这实际上是频率响应的xxx幅度。）H∞ 技术可用于最小化扰动的闭环影响：取决于 关于问题的制定，将根据稳定性或性能来衡量影响。

同时优化鲁棒性能和鲁棒稳定是困难的。 接近实现这一点的一种方法是 H∞ 环路整形，它允许控制设计人员将经典的环路整形概念应用于多变量频率响应以获得良好的稳健性能，然后优化系统带宽附近的响应以实现良好的 强大的稳定性。

商业软件可用于支持 H∞ 控制器综合。

首先，流程必须根据以下标准配置表示：

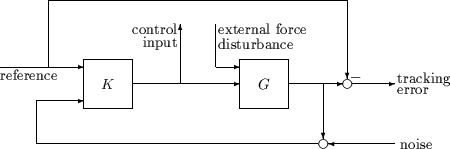
工厂 P 有两个输入，外生输入 w，包括参考信号和干扰，以及操纵变量 u。 有两个输出，我们要最小化的误差信号 z 和我们用来控制系统的测量变量 v。 v 在 K 中用于计算操纵变量 u。 请注意，所有这些通常都是向量，而 P 和 K 是矩阵。