电磁张量

在电磁学中，电磁张量或电磁场张量（有时称为场强张量、法拉第张量或麦克斯韦双矢量）是描述时空电磁场的数学对象。 场张量是在 Hermann Minkowski 引入狭义相对论的四维张量公式后首次使用的。 张量使得相关的物理定律可以写得非常简洁，并允许通过下面描述的拉格朗日公式对电磁场进行量化。

电磁张量，通常标记为 F，被定义为电磁四势 A 的外导数，微分 1 形式：

F = d e f d A。 {\displaystyle F\ {\stackrel {\mathrm {def} }{=}}\ \mathrm {d} A.}

因此，F是闵可夫斯基空间上的微分2-型，即反对称的2阶张量场。

其中 ∂ {\displaystyle \partial } 是四梯度，而 A {\displaystyle A} 是四势。

麦克斯韦方程的 SI 单位和粒子物理学家的 Minkowski 空间签名约定 (+ − − −)，将在本文通篇使用。

其中 d {\displaystyle d} 是外导数， {\displaystyle {\vec {J}}} 是 电流密度

而 ρ {\displaystyle \rho } 是电荷密度) 是 4-电流密度 1-形式，是麦克斯韦方程组的微分形式版本。

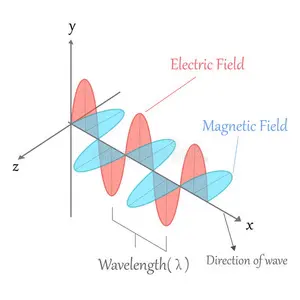
电场和磁场可以从电磁张量的分量中获得。

其中 ϵ i j k {\displaystyle \epsilon _{ijk}} 是 Levi-Civita 张量。 这给出了特定参考系中的场； 如果改变参考系，电磁张量的分量将发生协变变换，新参考系中的场将由新分量给出。