杜芬振子
词条百科 4
目录
杜芬振子
以 Georg Duffing(1861-1944 年)命名的杜芬振子(或 Duffing 振荡器)是一个非线性二阶微分方程,用于模拟某些阻尼和驱动振荡器。
该方程描述了阻尼振荡器的运动,其势比简谐运动更复杂(对应于 β = δ = 0 {displaystyle beta =delta =0} 的情况); 在物理方面,它模拟了一个弹性摆,其弹簧的刚度并不完全符合胡克定律。
杜芬振子是表现出混沌行为的动力系统的一个例子。 此外,Duffing系统在频率响应中呈现跳跃共振现象,这是一种频率滞后现象。
参数
上式中的参数为:
- δ {displaystyle delta } 控制阻尼量,
- α {displaystyle alpha } 控制线性刚度,
- β {displaystyle beta } 控制恢复力的非线性度; 如果 β = 0 , {displaystyle beta =0,} 杜芬振子描述了一个阻尼驱动的简谐振子,
- γ {displaystyle gamma } 是周期驱动力的振幅; 如果 γ = 0 {displaystyle gamma =0} 系统没有驱动力,并且
- ω {displaystyle omega } 是周期驱动力的角频率。
杜芬振子可以被看作是描述附加在非线性弹簧和线性阻尼器上的质量的振荡。
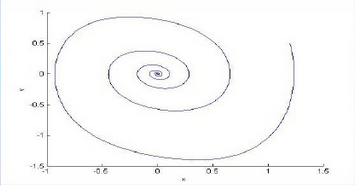
解决方法
一般来说,杜芬振子不承认精确的符号解。 然而,许多近似方法效果很好:
- 傅立叶级数的展开可以提供任意精度的运动方程。
- x 3 {displaystyle x{3}} 项,也称为 Duffing 项,可以近似为小项,系统可以视为受扰动的简谐振子。
- Frobenius 方法产生了一个复杂但可行的解决方案。
- 可以使用各种数值方法中的任何一种,例如 Euler 方法和 Runge–Kutta 方法。
- 同伦分析方法 (HAM) 也被报道用于获得杜芬振子的近似解,也用于强非线性。
在无阻尼( δ = 0 {displaystyle delta =0} )和无驱动。
内容来源于网络,本内容不代表16map.com立场,内容投诉举报请联系16map.com客服。如若转载,请注明出处:https://16map.com/wiki/nmzeaiwlmidc