有心力

在经典力学中，物体上的中心力是指向或远离称为力中心的点的力。

F → = F ( r ) = | F ( r ) | r ^ {displaystyle {vec {F}}=mathbf {F} (mathbf {r} )=leftvert F(mathbf {r} )right vert {hat {mathbf {r} }}}

其中 F → {textstyle {vec {F}}} 是力，F 是向量值力函数，F 是标量值力函数，r 是位置向量，||r|| 是它的长度，并且 r ^ = r / ‖ r ‖ {textstyle {hat {mathbf {r} }}=mathbf {r} /|mathbf {r} | } 是对应的单位向量。

并非所有的中心力场都是保守的或球对称的。 然而，中心力是保守的当且仅当它是球对称的或旋转不变的。

保守的有心力总是可以表示为势能的负梯度：-

F ( r ) = − ∇ V ( r ) ，其中 V ( r ) = ∫ | r | + ∞ F ( r ) d r {displaystyle mathbf {F} (mathbf {r} )=-mathbf {nabla } V(mathbf {r} ){text{, 其中 }}V(mathbf {r} )=int _{|mathbf {r} |}{+infty }F(r),mathrm {d} r}

（积分的上限是任意的，因为势能被定义为一个附加常数）。

在保守场中，总机械能（动能和势能）守恒：

E = 1 2 米 | r ˙ | 2 + 1 2 我 | ω | 2 + V ( r ) = 常数 {displaystyle E={frac {1}{2}}m|mathbf {dot {r}} |{2}+{frac {1} {2}}I|mathbf {omega } |{2}+V(mathbf {r} )={text{常数}}}

（其中 ‘ṙ’ 表示 ‘r’ 相对于时间的导数，即速度，’I’ 表示该物体的惯性矩， ‘ω’ 表示角速度），并且 在中心力场中，角动量也是如此：

L = r × m r ˙ = 常数 {displaystyle mathbf {L} =mathbf {r} times mmathbf {dot {r}} ={text{常数}}}

因为力施加的扭矩为零。 因此，物体在垂直于角动量矢量且包含原点的平面上运动，并服从开普勒第二定律。 （如果角动量为零，则物体沿着连接它与原点的直线移动。）

还可以证明，在任何中心力的影响下运动的物体服从开普勒第二定律。 然而，xxx和第三定律取决于牛顿万有引力定律的平方反比性质，一般不适用于其他中心力。

由于保守，这些特定的中心力场是无旋的，也就是说，它的旋度为零，除了原点：

∇ × F ( r ) = 0 。 {displaystyle nabla times mathbf {F} (mathbf {r} )=mathbf {0} {text{.}}}

引力和库仑力是两个熟悉的例子，其中 F ( r ) {displaystyle F(mathbf {r} )} 仅与 1/r2 成正比。 在这种具有负 F ( r ) {displaystyle F(mathbf {r} )}（对应于吸引力）的力场中的物体遵守开普勒行星运动定律。

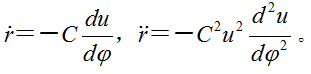
空间谐振子的力场位于 F ( r ) {displaystyle F(mathbf {r} )} 的中心，仅与 r 成正比且为负。

根据 Bertrand 定理，这两个 F ( r ) = − k / r 2 {displaystyle F(mathbf {r} )=-k/r{2}} 和 F ( r ) = − k r {displaystyle F(mathbf {r} )=-kr} 是所有有界轨道都是稳定闭合轨道的xxx可能的中心力场。 然而，还存在其他的力场，它们有一些封闭的轨道。