弗洛凯理论

弗洛凯理论是常微分方程理论的一个分支，涉及形式为周期性线性微分方程的解类

x ˙ = A ( t ) x , {displaystyle {dot {x}}=A(t)x,}

其中 A ( t ) {displaystyle displaystyle A(t)} 是周期为 T {displaystyle T} 的分段连续周期函数，并定义解的稳定性状态。

弗洛凯理论的主要定理，Floquet 定理，由 Gaston Floquet (1883) 提出，给出了该公共线性系统的每个基本矩阵解的规范形式。 它给出了坐标变化 y = Q − 1 ( t ) x {displaystyle displaystyle y=Q{-1}(t)x} 其中 Q ( t + 2 T ) = Q ( t ) {displaystyle displaystyle Q(t+2T)=Q(t)} 将周期系统转换为具有恒定实数系数的传统线性系统。

当应用于具有周期势能的物理系统时，例如凝聚态物理中的晶体，其结果被称为布洛赫定理。

请注意，线性微分方程的解形成一个向量空间。 如果所有列都是线性无关的解，则矩阵 ϕ ( t ) {displaystyle phi ,(t)} 称为基本矩阵解。 矩阵 Φ ( t ) {displaystyle Phi (t)} 称为主基本矩阵解，如果所有列都是线性独立的解并且存在 t 0 {displaystyle t_{0}} 使得 Φ ( t 0 ) {displaystyle Phi (t_{0})} 是恒等式。

令 x ˙ = A ( t ) x {displaystyle {dot {x}}=A(t)x} 为线性一阶微分方程，其中 x ( t ) {displaystyle x(t)} 是长度为 n {displaystyle n} 和 A ( t ) {displaystyle A(t)} 的列向量，一个 n × n {displaystyle ntimes n} 周期矩阵，周期为 T {displaystyle T}（即 A ( t + T ) = A ( t ) {displaystyle A(t+T)=A(t)} 对于 t {displaystyle t} 的所有实数值）。

这个映射 ϕ ( t ) = Q ( t ) e t R {displaystyle phi ,(t)=Q(t)e{tR}} 引起坐标随时间的变化 ( y = Q − 1 ( t ) x {displaystyle y=Q{-1}(t)x} )，在此条件下，我们的原始系统变成了具有实常系数 y ˙ = R y {displaystyle {dot {y}}=Ry}。 由于 Q ( t ) {displaystyle Q(t)} 是连续且周期性的，因此它必须是有界的。 因此，y ( t ) {displaystyle y(t)} 和 x ( t ) {displaystyle x(t)} 的零解的稳定性由 R {displaystyle R} 的特征值决定。

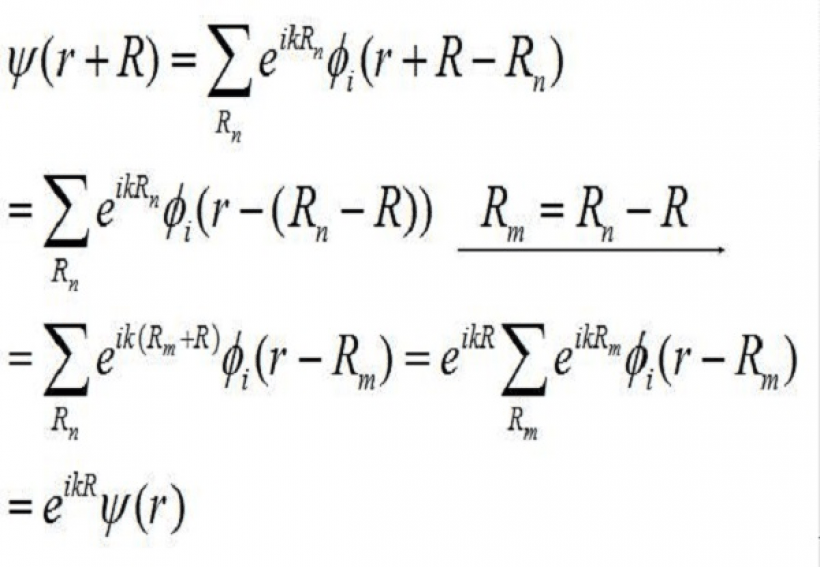
表示 ϕ ( t ) = P ( t ) e t B {displaystyle phi ,(t)=P(t)e{tB}} 称为基本矩阵 ϕ ( t ) 的 Floquet 范式 {displaystyle phi ,(t)} 。

e T B {displaystyle e{TB}} 的特征值称为系统的特征乘数。 它们也是（线性）庞加莱映射 x ( t ) → x ( t + T ) {displaystyle x(t)to x(t+T)} 的特征值。 Floquet 指数（有时称为特征指数）是复数 μ {displaystyle mu } 使得 e μ T {displaystyle e{mu T}} 是系统的特征乘数。 请注意 Floquet 指数不是xxx的，因为 e ( μ + 2 π i k T ) T = e μ T {displaystyle e{(mu +{frac {2pi ik}{T}}) T}=e{mu T}} ，其中 k {displaystyle k} 是一个整数。