压缩因子

系统属性注意：共轭变量以斜体显示

材料特性

• 属性数据库

可压缩性 β = − {displaystyle beta =-}
热膨胀 α = {displaystyle alpha =}

方程式

• 卡诺定理
• 克劳修斯定理
• 基本关系
• 理想气体定律

• 麦克斯韦关系
• Onsager 互惠关系
• 布里奇曼方程
• 热力学方程表

潜力

• 自由能
• 自由熵

• 内能 U ( S , V ) {displaystyle U(S,V)}
• 焓 H ( S , p ) = U + p V {displaystyle H(S,p)=U+pV}
• 亥姆霍兹自由能 A ( T , V ) = U − T S {displaystyle A(T,V)=U-TS}
• 吉布斯自由能 G ( T , p ) = H − T S {displaystyle G(T,p)=H-TS}

• 历史
• 文化

科学家们

• 伯努利
• 玻尔兹曼
• 布里奇曼
• 卡拉西奥多里
• 卡诺
• 克拉佩龙
• 克劳修斯
• 德唐德
• 迪昂
• 吉布斯
• 冯·亥姆霍兹
• 焦耳
• 刘易斯
• 马修
• 麦克斯韦
• 冯迈耶
• 能斯特
• 昂萨格
• 普朗克
• 兰金
• 史密顿
• 斯塔尔
• 泰特
• 汤普森
• 汤姆逊
• 范德瓦尔斯
• 沃特斯顿

其他

• 成核
• 自组装
• 自组织
• 秩序与混乱

• 类别

• v
• t
• e

在热力学中，压缩系数 (Z)，也称为压缩系数或气体偏差系数，描述了实际气体与理想气体行为的偏差。 简单定义为在相同温度和压力下，气体的摩尔体积与理想气体的摩尔体积之比。 它是一种有用的热力学性质，可用于修改理想气体定律以解释实际气体行为。 一般来说，气体越接近相变、温度越低或压力越大，与理想行为的偏差就变得越明显。 压缩因子值通常通过状态方程 (EOS) 的计算获得，例如以化合物特定经验常数作为输入的维里方程。 对于两种或多种纯气体（例如空气或天然气）的混合物的气体，必须先知道气体成分，然后才能计算可压缩性。 或者，可以从广义压缩率图表中读取特定气体的压缩系数，该图表将 Z {displaystyle Z} 绘制为恒定温度下压力的函数。

压缩系数不应与材料的可压缩性（也称为可压缩系数或等温可压缩性）混淆，后者是衡量流体或固体响应压力变化的相对体积变化的量度。

压缩因子在热力学和工程学中通常定义为：

其中 p 是压力，ρ {displaystyle rho } 是气体的密度，R specific = R M {textstyle R_{text{specific}}={frac {R}{M} }} 是特定气体常数，M {displaystyle M} 是摩尔质量，T {displaystyle T} 是xxx温度（开尔文或朗肯标度）。

在统计力学中的描述是：

其中 p 是压力，n 是气体的摩尔数，T {displaystyle T} 是xxx温度，R {displaystyle R} 是气体常数。

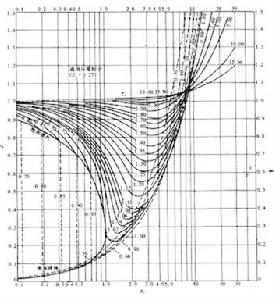
对于理想气体，根据定义，压缩系数为 Z = 1 {displaystyle Z=1}。 在许多现实世界的应用中，对精度的要求要求考虑与理想气体行为（即真实气体行为）的偏差。 Z {displaystyle Z} 的值通常随压力增加而随温度降低。 在高压下，分子碰撞的频率更高。 这使得分子间的排斥力产生明显的影响， 当压力较低时，分子可以自由移动。 在这种情况下，吸引力占主导地位 . 气体越接近其临界点或沸点， 就越偏离理想情况。