乘积累加运算
目录
乘积累加运算
在计算,尤其是数字信号处理中,乘加 (MAC) 或乘加 (MAD) 运算是计算两个数的乘积并将该乘积添加到累加器的常见步骤。 执行运算的硬件单元称为乘法累加器(MAC 单元); 该操作本身通常也称为 MAC 或 MAD 操作。 MAC 操作修改累加器 a:
a ← a + ( b × c )
当处理浮点数时,可能会执行两次舍入(在许多 DSP 中很典型),或一次舍入。 当执行单次舍入时,它称为融合乘加 (FMA) 或融合乘加 (FMAC)。
现代计算机可能包含一个专用的 MAC,包括一个以组合逻辑实现的乘法器,后跟一个加法器和一个存储结果的累加器寄存器。 寄存器的输出被反馈到加法器的一个输入,因此在每个时钟周期,乘法器的输出被添加到寄存器。 组合乘法器需要大量逻辑,但可以比早期计算机的典型移位和加法更快地计算乘积。
在浮点运算中
当用整数完成时,操作通常是精确的(计算模数 2 的幂)。 然而,浮点数只有一定的数学精度。 也就是说,数字浮点运算通常不是关联的或分配的。 (请参阅浮点数§精度问题。)因此,乘加运算是通过两次舍入执行,还是在一次运算中进行一次舍入(融合乘加运算),结果会有所不同。
融合乘加
融合乘加(FMA 或 fmadd)是一种单步舍入的浮点乘加运算。 也就是说,一个未融合的乘加法将计算乘积 b × c,将其四舍五入为 N 个有效位,将结果加到 a,然后四舍五入为 N 个有效位,而一个融合乘法加法将计算整个表达式 a + (b × c) 在将最终结果四舍五入到 N 个有效位之前达到其全精度。
快速 FMA 可以加速和提高许多涉及乘积累积的计算的准确性:
通常可以依靠融合乘加来提供更准确的结果。 然而,William Kahan 指出,如果不加思索地使用它可能会产生问题。 如果 x2 − y2 被计算为 ((x × x) − y × y)(遵循 Kahan 建议的符号,其中多余的括号指示编译器首先舍入 (x × x) 项)使用融合乘加, 那么即使 x = y 由于xxx次乘法丢弃了低有效位,结果也可能为负。 这可能会导致错误,例如,如果随后计算结果的平方根。
当在微处理器内部实现时,FMA 可以比乘法运算后加法更快。 然而,基于原始 IBM RS/6000 设计的标准工业实现需要 2N 位加法器才能正确计算总和。
包含此指令的另一个好处是,它允许高效的软件实现除法(请参阅除法算法)和平方根(请参阅计算平方根的方法)操作,从而无需为这些操作使用专用硬件。
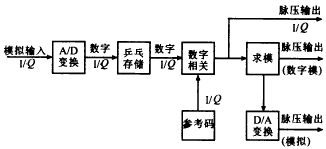
点积指令
一些机器将多个融合乘加操作组合成一个步骤,例如 在两个 128 位 SIMD 寄存器 a0×b0 + a1×b1 + a2×b2 + a3×b3 上以单周期吞吐量执行四元素点积。
支持
FMA 操作包含在 IEEE 754-2008 中。
Digital Equipment Corporation (DEC) VAX 的 POLY 指令用于使用连续的乘法和加法步骤根据 Horner 规则计算多项式。 指令说明未指定乘法和加法是否使用单个 FMA 步骤执行。