佩特里网

佩特里网，也称为位置/转换 (PT) 网，是用于描述分布式系统的几种数学建模语言之一。 它是一类离散事件动态系统。 佩特里网是一个有向二分图，它有两种类型的元素，位置和转移。 Place 元素被描绘为白色圆圈，Transition 元素被描绘为矩形。 一个地方可以包含任意数量的标记，用黑色圆圈表示。 如果作为输入连接到它的所有位置都包含至少一个标记，则启用转换。 一些消息来源指出，佩特里网是 1939 年 8 月由年仅 13 岁的 Carl Adam Petri 发明的，目的是描述化学过程。

与 UML 活动图、业务流程模型和表示法以及事件驱动流程链等行业标准一样，佩特里网为包括选择、迭代和并发执行在内的逐步流程提供图形表示法。 与这些标准不同，佩特里网对其执行语义有精确的数学定义，并具有用于过程分析的完善的数学理论。

德国计算机科学家卡尔·亚当·佩特里（Carl Adam Petri）在其 1962 年的论文《自动化与通讯》中对佩特里网进行了广泛分析，此类结构就是以他的名字命名的。

佩特里网由位置、过渡和弧组成。 弧从一个地方运行到一个过渡，反之亦然，从不在地方之间或在过渡之间。 弧运行到过渡的地方称为过渡的输入位置； 弧从过渡运行到的位置称为过渡的输出位置。

从图形上看，佩特里网中的地点可能包含离散数量的标记，称为标记。 代币在这些地方的任何分布都将代表一种称为标记的网络配置。 在与佩特里网图相关的抽象意义上，佩特里网的转换可能会在启用时触发，即在其所有输入位置都有足够的标记； 当转换触发时，它会消耗所需的输入令牌，并在其输出位置创建令牌。 一次触发是原子的，即一个不可中断的步骤。

除非定义了执行策略（例如严格的转换顺序，描述优先级），佩特里网的执行是不确定的：当同时启用多个转换时，它们将以任何顺序触发。

由于触发是不确定的，并且多个令牌可能出现在网络中的任何地方（甚至在同一个地方），佩特里网非常适合对分布式系统的并发行为进行建模。

佩特里网是状态转换系统，它扩展了一类称为基本网络的网络。

定义 1. 网络是一个元组 N = ( P , T , F ) {displaystyle N=(P,T,F)} 其中

• P {displaystyle P} 和 T {displaystyle T} 分别是位置和转移的不相交有限集。
• F ⊆ ( P × T ) ∪ ( T × P ) {displaystyle Fsubseteq (Ptimes T)cup (Ttimes P)} 是一组（有向）弧 （或流动关系）。

定义 2. 给定网络 N = (P, T, F)，配置是集合 C，使得 C ⊆ P。

定义 3. 基本网络是 EN = (N, C) 形式的网络，其中

• N = (P, T, F) 是一个网。
• C 使得 C ⊆ P 是一个构型。

定义 4. 佩特里网是形式为 PN = (N, M, W) 的网络，它扩展了基本网络，使得

• N = (P, T, F) 是一个网。
• M：P → Z 是一个位置多重集，其中 Z 是一个可数集。 M 扩展了配置的概念，通常参考佩特里网图作为标记进行描述。
• W : F → Z 是弧多重集，因此每个弧的计数（或权重）是弧多重性的度量。

如果一个佩特里网等价于一个初等网，则Z可以是可数集{0,1}，P中那些映射到M下1的元素构成一个构型。 类似地，如果佩特里网不是基本网络，则多重集 M 可以解释为表示非单例配置集。 在这方面，M 将基本网络的配置概念扩展到佩特里网。

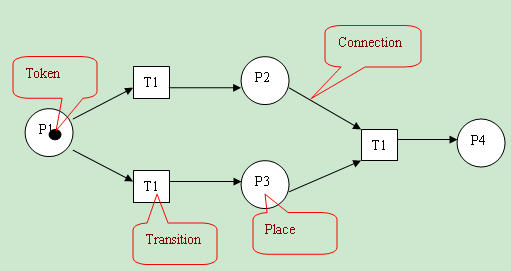
在佩特里网的图表中，地方通常用圆圈表示，过渡用长而窄的矩形和弧形作为单向箭头，显示地方到过渡或过渡到地方的连接。 如果该图是一个基本网络，那么配置中的那些地方通常会被描绘成圆圈，其中每个圆圈包含一个称为令牌的点。 在佩特里网的给定图表中（见右图），地点圆圈可能包含多个标记，以显示一个地点在配置中出现的次数。 分布在整个佩特里网图上的令牌配置称为标记。

p1 处是转换 t 的输入处； 而位置 p2 是同一转换的输出位置。