伯恩斯坦多项式
词条百科 0
目录
伯恩斯坦多项式
在数学领域的数值分析中,伯恩斯坦多项式是一个多项式,是伯恩斯坦基础多项式的线性组合。这个想法是以谢尔盖-纳塔诺维奇-伯恩斯坦命名的。评估伯恩斯坦形式的多项式的一个稳定的数字方法是deCasteljau的算法。伯恩斯坦首次将伯恩斯坦形式的多项式用于Weierstrass近似定理的构造证明中。随着计算机图形学的出现,局限于区间[0,1]的伯恩斯坦多项式在贝塞尔曲线的形式上变得非常重要。
伯恩斯坦多项式的定义
n+1度的伯恩斯坦基础多项式定义为n度的伯恩斯坦基础多项式构成了向量空间的基础{displaystyle`Pi_{n}}度数为n的多项式的向量空间的基。的实系数度数最多为n的多项式的基础。伯恩斯坦基础多项式的线性组合被称为伯恩斯坦多项式或伯恩斯坦形式的n度多项式。{displaystyleβ_{nu}}称为伯恩斯坦系数。被称为Bernstein系数或Bézier系数。上面的前几个单项式的伯恩斯坦基础多项式是。
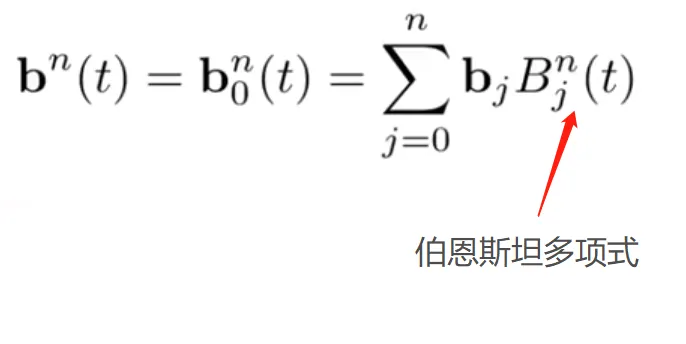
伯恩斯坦多项式的特性
伯恩斯坦基数多项式具有以下特性。伯恩斯坦多项式向单项式的转化是b
内容来源于网络,本内容不代表16map.com立场,内容投诉举报请联系16map.com客服。如若转载,请注明出处:https://16map.com/wiki/nmteyi4lnitk