同调回归

在统计学和数字分析中，同调回归或单调回归是将一条自由形式的线拟合到一连串的观测值上的技术，使拟合的线在任何地方都不递减（或不递增），并尽可能地接近于观测值。

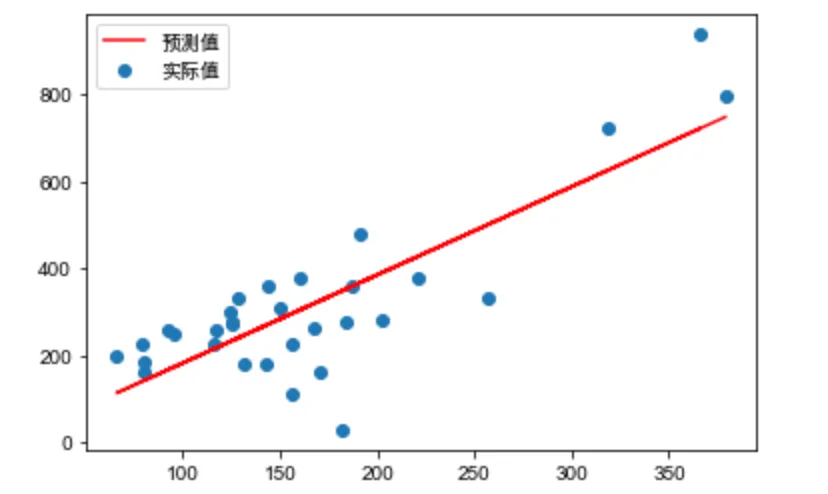
同调回归在统计推理中得到了应用。例如，当一组实验结果的平均值按照某种特定的顺序增加时，人们可以用它来拟合一条等调曲线。等价回归的一个好处是，它不受任何函数形式的限制，例如线性回归所强加的线性，只要函数是单调的增加。另一个应用是非度量的多维缩放，其中寻求数据点的低维嵌入，使嵌入中各点之间的距离顺序与各点之间的不相似性顺序一致。同调回归被反复用来拟合理想的距离，以保持相对的异同度顺序。同调回归也被用于概率分类，以校准监督机器学习模型的预测概率。单变量的简单有序情况下的等值回归x,y{displaystylex,y}已被应用于估计麻醉学和毒理学等领域的连续剂量-反应关系。狭义地讲，等值回归只提供在观察值为x.{displaystylex.}。在没有任何额外假设的情况下，完整的剂量-反应曲线的估计通常是通过点估计之间的线性插值完成的。已经为R、Stata和Python开发了计算同调（单调）回归的软件。

{displaystylex_{i}}的部分排序。(并可被视为一些有向无环图（dag）的边的集合，其顶点为1,2,…n{displaystyle1,2,ldotsn}。).这种形式的问题可以通过一般的二次编程技术来解决。{displaystylex_{i}}的值属于一个完全有序的集合，如值落在一个完全有序的集合中，如R{displaystylemathbb{R}}，我们可以假设WLOG的观测值已经被排序，从而使其成为一个完全有序的集合。我们可以假设WLOG的观测值已经被排序，以便.在这种情况下，解决二次方程序的简单迭代算法是池相邻违规者算法。相反，Best和Chakravarti将该问题作为一个主动集合识别问题来研究，并提出了一个原始算法。这两种算法可以被看作是彼此的对偶，两者的计算复杂度为{displaystylex_{i}inmathbb{R}}时，常见的选择是在点与点之间进行线性插值。将是在各点之间进行线性内插