多变量适应性回归样条

在统计学中，多变量适应性回归样条（MARS）是由JeromeH.Friedman在1991年提出的一种回归分析形式。它是一种非参数回归技术，可以被看作是线性模型的延伸，可以自动建立非线性和变量间的相互作用。

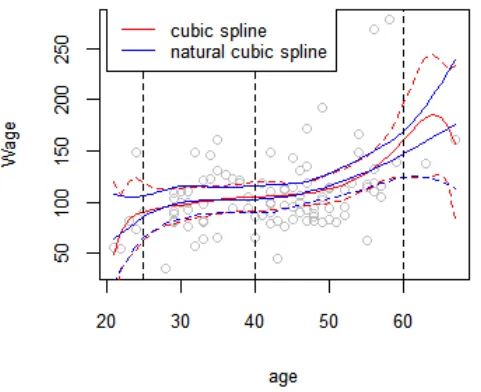
本节通过几个例子来介绍MARS。我们从一组数据开始：输入变量的矩阵x，以及观察到的响应的向量y，x中的每一行都有一个响应，例如，数据可以是。这里只有一个自变量，所以x矩阵只是一个单列。鉴于这些测量结果，我们想建立一个模型，预测给定x的预期y。x的极值的数据表明，y和x之间的关系可能是非线性的（看看相对于x的低值和高值的回归线的红点）。因此，我们求助于MARS来自动建立一个考虑到非线性因素的模型。MARS软件从给定的x和y构建一个模型，如下所示与x的关系，y的原始值再次显示为红点。预测的响应现在更适合于原始y值。MARS在预测的y中自动产生了一个扭结，以考虑到非线性的因素。这个扭结是由铰链函数产生的。铰链函数是以下列开头的表达式在这个简单的例子中，我们可以很容易地从图中看到y与x有非线性关系（也许可以猜到y随x的平方而变化）。然而，在一般情况下，会有多个自变量，y和这些变量之间的关系并不明确，不容易通过绘图看到。我们可以用MARS来发现这种非线性关系。

一个有多个变量的MARS表达式的例子是这个表达式将空气污染（臭氧水平）作为温度和其他一些变量的函数。请注意，公式中的最后一项（在最后一行）包含了以下因素的相互作用变化，其他变量固定在它们的中值。图中显示，除非能见度低，否则风不会影响臭氧水平。我们看到，MARS可以通过组合铰链函数建立相当灵活的回归面。为了得到上述表达式，MARS模型建立程序自动选择使用哪些变量（有些变量很重要，有些则不重要），选择铰链函数的结点位置，以及铰链函数的组合方式。

MARS建立的模型形式为{displaystyleB_{i}(x)}是以下三种形式之一采取以下三种形式之一。1）一个常数1。只有一个这样的项，即截距。