可识别性分析

可识别性分析是在数理统计中发现的一组方法，用于确定一个模型的参数由实验数据的数量和质量来估计的程度。因此，这些方法不仅探讨了模型的可识别性，而且还探讨了模型与特定实验数据的关系，或者更广泛地探讨了数据收集过程。

假设一个模型适合于实验数据，拟合度并不能揭示参数估计的可靠性。拟合度也不足以证明模型的选择是正确的。例如，如果实验数据是有噪声的，或者数据点的数量不足，那么参数的估计值可能会有很大的变化而不会对拟合优度产生明显的影响。为了解决这些问题，可识别性分析可以作为一个重要步骤来应用，以确保正确选择模型和足够数量的实验数据。这种分析的目的是对正确的模型选择和获得的实验数据的完整性进行量化证明，或者这种分析可以作为检测不可识别的和马虎的参数的工具，帮助规划实验，在早期阶段建立和改进模型。

结构可识别性分析是一种特殊的分析类型，在这种分析中，模型结构本身被调查为不可识别性。确认的不可识别性可以通过用它们的组合替代不可识别的参数或通过其他方式来分析消除。模型在应用于模拟有限实验数据集后，其独立参数的数量过多，可能会对实验数据提供良好的拟合，代价是使拟合结果对参数值的变化不敏感，从而使参数值无法确定。

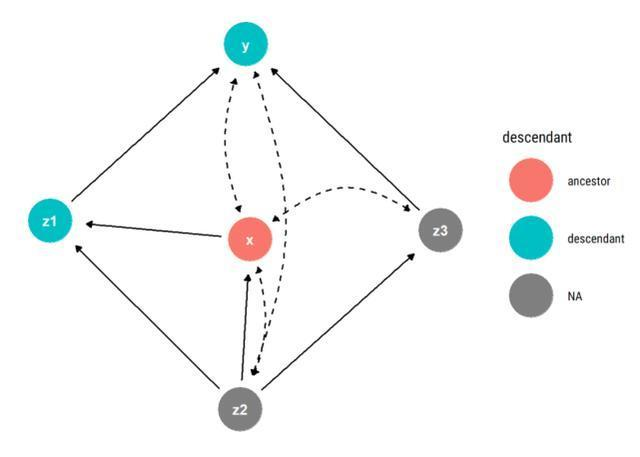
结构方法也被称为先验方法，因为在这种情况下，非可识别性分析也可以在计算拟合分数函数之前进行，通过探索模型的自由度（统计量）数量和要变化的独立实验条件数量。实际的可识别性分析可以通过探索现有模型与实验数据的拟合来进行。一旦获得任何措施的拟合，参数可识别性分析可以在给定点附近（通常在提供最佳模型拟合的参数值附近）进行局部分析，也可以在扩展的参数空间上进行全局分析。实际可识别性分析的常见例子是轮廓似然法。