无差拍控制
词条百科 30
目录
无差拍控制
在离散时间控制理论中,无差拍控制问题包括找出必须向系统施加什么输入信号才能使输出在最少的时间步长内达到稳定状态。
对于 N 阶线性系统,可以证明该最小步数最多为 N(取决于初始条件),前提是该系统是零可控的(可以通过某些输入使其状态为零) . 解决方案是应用反馈,使闭环传递函数的所有极点都位于 z 平面的原点。 (有关传递函数和 z 平面的更多信息,请参阅 z 变换)。 因此线性情况很容易解决。 通过扩展,在原点处具有传递函数的所有极点的闭环传递函数有时称为无差拍传递函数。
对于非线性系统,无差拍控制是一个开放的研究问题。
由于其良好的动态特性,无差拍控制器常用于过程控制。 它们是经典的反馈控制器,其中控制增益是使用基于工厂系统阶数和归一化自然频率的表格来设置的。
无响应响应具有以下特征:
- 零稳态误差
- 最短上升时间
- 最短稳定时间
- 少于 2% 的过冲/下冲
- 非常高的控制信号输出
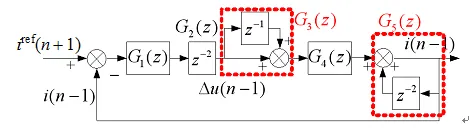
传递函数
考虑植物的传递函数
和离散时间延迟 e − d {displaystyle e{-d}} 。
闭环传递函数计算为
L(z)=B(z)B(1)。 {displaystyle mathbf {L} (z)={frac {B(z)}{B(1)}}。}
内容来源于网络,本内容不代表16map.com立场,内容投诉举报请联系16map.com客服。如若转载,请注明出处:https://16map.com/wiki/nmjeai4lmidc